6.4 Последовательность частей задач

Для большинства программ обучения подходит последовательность целостных задач, в результате получается предварительный план обучения, подобный представленному в таблицах 6.1 и 6.2. В исключительных случаях, однако, может оказаться невозможным найти достаточно простой класс задач для начала обучения — нужна довольно длительная подготовка, прежде чем учащиеся смогут приступить к выполнению первой учебной задачи. Так обстоят дела с полными образовательными программами (то есть учебными планами) для врачей, пилотов или юристов. В этом случае (но только в этом случае!) в дополнение к последовательности целостных задач используется последовательность частей задач. Если это не так, вы можете пропустить этот раздел.

Для последовательности частей задач необходимо определить порядок, в котором в ходе обучения будут рассматриваться кластеры базовых навыков (то есть части). Последовательность частей задач очень эффективна для снижения сложности задачи, но может мешать интеграции знаний, навыков и установок и ограничивает координацию базовых навыков (Wickens et al., 2013), поэтому ее следует использовать с осторожностью.

Кластеры навыков как простые части

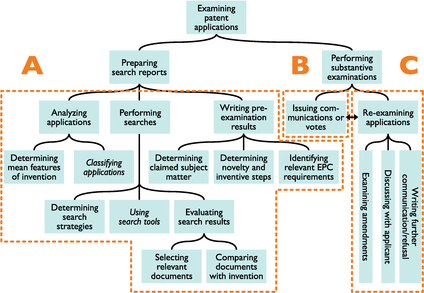
Рис. 6.4 Три кластера навыков для очень сложного навыка «экспертиза патентных заявок». Часть А состоит из подготовки отчетов о поиске и навыков более низкого уровня, часть В состоит из оповещения или голосования, часть С состоит из повторной экспертизы заявок и навыков более низкого уровня

Если экспертная оценка указывает на то, что подготовка новых стажеров даже к первому классу задач в области патентной экспертизы (согласно таб. 6.1 это область четких заявок с одним независимым пунктом, четким и полным ответом заявителя и без необходимости пересмотра в порядке промежуточного рассмотрения) займет много недель, может потребоваться подход последовательности частей задач. Сначала определяется небольшое количество кластеров навыков (обычно от двух до пяти), которые представляют собой наборы значимо взаимосвязанных базовых навыков. Чем меньше количество кластеров навыков, или частей, тем лучше, поскольку это дает больше возможностей для интеграции и координации знаний, навыков и установок. Выбранные кластеры должны позволять учащимся в разумные сроки приступить к реальной практике (например, в течение нескольких часов или дней), каждый кластер должен сам по себе отражать аутентичную, реальную жизненную задачу. Например, три содержательно взаимосвязанные части целостного навыка «экспертиза патентных заявок» (см. рис. 6.4) — это ветви «подготовка отчетов о поиске» (часть А), «оповещение или голосование» (часть В) и «повторная экспертиза заявок» (часть С).

Прямая и обратная цепочка рассуждений с использованием метода снежного кома и без него

Два основных подхода к последовательности частей задач — это прямая цепочка рассуждений и обратная цепочка рассуждений. Прямая цепочка рассуждений располагает части в том же порядке, в котором они возникают при обычном выполнении задачи. Она может принимать две различные формы, а именно с использованием метода снежного кома (опираясь на предыдущее и, таким образом, становясь больше, подобно снежному кому, который растет, скатываясь с горы) и без него. Простая прямая цепочка рассуждений (A — B — C) рассматривает части по одной. В нашем примере можно начать с обучения подготовке отчетов о поиске (часть А), затем продолжить обучение оповещению и голосованию (часть В) и закончить обучением повторной экспертизе заявок (часть С). Обратите внимание, что при этом подходе учащиеся никогда не отрабатывают задачу целиком. Когда они практикуют оповещение или голосование, они обычно делают это на основе отчетов, которые они подготовили на предыдущем этапе, а когда они практикуют повторное рассмотрение заявок, они обычно делают это на основе отчетов, рассылок или голосований, которые они подготовили на двух предыдущих этапах. Прямая цепочка рассуждений с использованием метода снежного кома (A — AB — ABC) включает предыдущую часть (части) в каждую новую часть. В нашем примере можно начать с обучения подготовке отчетов о поиске (часть А), затем продолжить обучением подготовке отчетов о поиске плюс оповещению или голосованию (часть АВ) и закончить подготовкой отчетов о поиске плюс оповещением или голосованием плюс повторной экспертизой заявок (АВС, что и составляет всю задачу). Как правило, метод снежного кома удлиняет обучение, но это более чем оправдывает себя, поскольку дает лучшие возможности для интеграции и обучения координации различных кластеров навыков (частей).

При обратной цепочке рассуждений мы имеем дело с частями целостной задачи в обратном или неправильном порядке. Как и прямая цепочка рассуждений, она может принимать две различные формы. Простая обратная цепочка рассуждений (CAB — BA — A) рассматривает части по одной. В нашем примере можно начать с обучения повторной экспертизе заявок (часть CAB), затем продолжить обучение оповещению или голосованию (часть BA) и закончить обучением подготовке отчетов о поиске (часть A). Как и в простой прямой цепочке рассуждений, учащиеся никогда не отрабатывают задачу целиком, но они могут приступить к части С, только получив готовые отчеты о поиске, оповещении и голосовании, поскольку они не выполняли эти части самостоятельно. На это указывают подстрочные символы: CAB означает, что учащиеся пересматривают заявки на основе отчетов о поиске, рассылок и результатов голосования, выданных инструктором или включенных в программу обучения, а BA — что они занимаются оповещением или голосованием на основе отчетов о поиске, выданных инструктором или включенных в программу обучения. Обратная цепочка рассуждений с использованием метода снежного кома (CAB — BCA — ABC) включает предыдущую часть (части) в каждую новую часть. В нашем примере обучение начинается с повторной экспертизы заявок на основе готовых отчетов о поиске плюс рассылок и результатов голосований (часть CAB); продолжается оповещением или голосованием плюс повторной экспертизой заявок на основе готовых отчетов о поиске (часть BCA) и заканчивается подготовкой отчетов о поиске плюс оповещением или голосованием плюс повторной экспертизой заявок (ABC, то есть вся задача). В таблице 6.3 обобщены четыре метода последовательности частей задачи и представлены рекомендации по их использованию.

Рекомендации в таблице 6.3 основаны на двух принципах. Во-первых, последовательность с методом снежного кома более эффективна, чем без него, поскольку она дает учащимся возможность практиковаться в выполнении всей задачи (то есть ABC) и таким образом помогает им научиться интегрировать и координировать различные части задачи. Следовательно, метод снежного кома следует использовать, если позволяет учебное время. Во-вторых, обратная цепочка рассуждений более эффективна, чем прямая, потому что она сталкивает обучающихся с полезными примерами и моделями для всей задачи с самого начала программы обучения. Например, если учащиеся сначала практикуются в повторной экспертизе патентных заявок на основе предоставленных отчетов о поиске, рассылок и результатов голосований, они увидят и изучат множество полезных примеров отчетов о поиске, оповещений и голосований к тому времени, когда начнут практиковаться в подготовке этих документов самостоятельно. Следует отметить, что эти принципы неприменимы к последовательности выполнения практических задач в рамках частичной практики (см. шаг 10 в главе 13).

Таблица 6.3 Техники последовательности частей задач с рекомендациями

Примечание: все эти техники следует использовать только в исключительном случае, если невозможно найти целостные задачи, достаточно простые для начала обучения.

Некоторые исследования показали, что обратная цепочка рассуждений с использованием метода снежного кома может быть очень эффективной стратегией. В одном из старых исследований Гроппер (1973) использовал ее для обучения проектированию обучающих систем. Вначале учащиеся оценивали и пересматривали учебные материалы (традиционно последняя часть дизайна обучения). Они получали смоделированные результаты для задач проектирования, начиная от описания задач и заканчивая разработкой материалов. На последующих этапах студенты учились проектировать и разрабатывать учебные материалы. Эта стратегия оказалась очень эффективной, поскольку учащиеся имели возможность ознакомиться с несколькими смоделированными продуктами, прежде чем от них потребовали самостоятельного выполнения таких задач, как формулирование стратегии, создание последовательности или анализ задач. В том же ключе ван Мариенбор и Краммер (1987) описали обратную цепочку рассуждений и метод снежного кома для обучения компьютерному программированию. Вначале учащиеся оценивали существующее ПО посредством тестирования, чтения и ручной трассировки (то есть традиционно последней части процесса разработки). На втором этапе они модифицировали, дополняли и масштабировали существующие проекты, и только на третьем этапе они проектировали и разрабатывали новое ПО с нуля. Эта стратегия была намного эффективнее, чем традиционное построение прямой цепочки рассуждений, — вероятно, потому, что учащиеся могли опереться на многочисленные модели и примеры программ, которые они уже знали.

Последовательность «целое — часть» в сравнении с последовательностью «часть — целое»

Последовательность целостных задач и последовательность частей задач могут быть объединены двумя способами, а именно в последовательности «целое — часть» и в последовательности «часть — целое» (см. рис. 6.5).

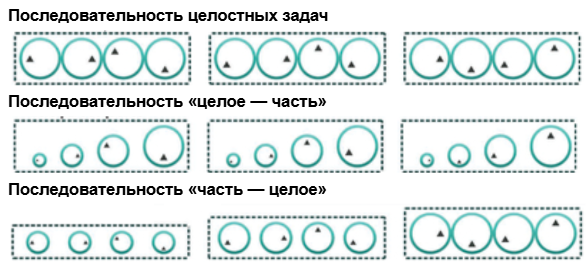
Рис. 6.5 Схематическое изображение обычной последовательности целостных задач, последовательности «целое — часть» и последовательности «часть — целое». Меньшие круги обозначают части всей задачи

При последовательности «целое — часть» сначала разрабатывают последовательность классов задач от простых к сложным с целостными задачами, используя упрощающие условия, направление фокуса внимания и развитие знания (Mulder et al., 2011; Si & Kim, 2011). Если окажется, что первый класс задач все еще слишком сложен для начала обучения, можно использовать технику последовательности частей задач, чтобы разделить первый и другие классы задач на кластеры или части от базовых к сложным навыкам. Основная идея заключается в том, чтобы начать с последовательности целостных задач от простого к сложному и только затем разделить ее на части. В последовательности «часть — целое», напротив, сначала разрабатывается последовательность частей или кластеров навыков от простого к сложному. Если первая часть или кластер навыков слишком сложны для начала обучения, можно использовать технику последовательности целостных задач для создания дальнейшей последовательности частей от простого к сложному в классах задач. Обратите внимание, что термин «последовательность целостных задач» выглядит путано, поскольку он относится к одной части или кластеру навыков так, будто это целостная задача.

В таблице 6.4 сравниваются последовательности «целое — часть» и «часть — целое». Есть три класса задач от простого к сложному (ABC — целое); три кластера навыков от простого к сложному с обратной цепочкой рассуждений и методом снежного кома (CAB, BCA, ABC — части) и три учебные задачи со снижением степени поддержки от высокой до ее отсутствия для каждой комбинации класса задач и кластера навыков. Явное преимущество последовательности «целое — часть» (левая колонка) перед последовательностью «часть — целое» (правая колонка) заключается в том, что в подходе «целое — часть» учащиеся получают возможность относительно быстро отработать задачу (обозначенную заштрихованными клетками) целиком. Это должно помочь интеграции и координации. Кроме того, последовательность «целое — часть» позволяет легко перейти к последовательности целостных задач на более поздних этапах программы обучения. Например, можно использовать последовательность «целое — часть» в первом классе задач, а затем перейти к последовательности целостных задач, удалив клетки CABms и BCAmm из второго класса задач и CABcs и BCAcm из третьего класса задач. Такой переход невозможен в последовательности «часть — целое».

Подводя итог, можно сказать, что последовательность «целое — часть» дает лучшие координацию и интеграцию, чем последовательность «часть — целое», и поэтому предпочтительна для сложных учебных задач. Последовательность «часть — целое» следует рассматривать только в том случае, если навыки сложны для изучения, но требуемая координация базовых навыков незначительна, что может быть справедливо для очень сложных повторяющихся базовых навыков (примеры см. в шаге 10 в главе 13).

Таблица 6.4 Сравнение последовательности «целое — часть» (от классов задач к кластерам навыков) и последовательности «часть — целое» (от кластеров навыков к классам задач). Кластеры навыков основаны на обратной цепочке рассуждений с использованием метода снежного кома

В таблице 6.5 приведен пример последовательности «целое — часть» в обучении патентной экспертизе. Он начинается с двух классов задач, идентичных классам задач, представленным в таблице 6.1 (левая колонка). В первом классе задач учащиеся рассматривают ясные заявки с одиночными независимыми пунктами формулы изобретения, четкие и полные ответы без необходимости промежуточной экспертизы. Во втором классе задач они по-прежнему имеют дело с ясными заявками из одиночных независимых пунктов, но появляются неясные и неполные ответы заявителя, а также необходимость в промежуточной экспертизе. Каждый класс задач теперь дополнительно разделен на три подкласса, представляющих части задачи, которые выполняются в следующем порядке. Учащиеся: а) повторно рассматривают заявки на основе предоставленных отчетов о поиске, рассылок и результатов голосования; б) проводят оповещение или голосование, повторно рассматривают заявки на основе предоставленных отчетов о поиске; в) готовят отчеты о поиске, проводят оповещение или голосование, повторно рассматривают заявки. Таким образом, каждый класс задач завершается выполнением целостной задачи на все более высоком уровне сложности.

Таблица 6.5 Два класса целостных задач, с тремя кластерами навыков (частями) каждый, для навыка патентной экспертизы, основанные на последовательности «целое — часть» и обратной цепочке рассуждений с использованием метода снежного кома для частей