4.6 Встроенная поддержка задач

Различные типы учебных задач обеспечивают различную поддержку, предоставляя разное количество информации об исходном состоянии, целевом состоянии и решении. На одном конце континуума находятся обычные задачи, в которых учащийся сталкивается только с заданным состоянием и набором критериев достижения цели (например, получить 98%-й спирт из исходных компонентов). Обычные задачи не оказывают обучающемуся никакой поддержки (то есть не предоставляют части решения), он должен сам выработать правильное решение. Как показано в верхней части рисунка 4.6, обычные задачи принимают разные формы в зависимости, с одной стороны, от их структуры и однозначности решения и, с другой стороны, от учащегося. Обычная задача может быть хорошо структурирована и иметь только одно приемлемое решение (например, найти сумму десятичных чисел 15 и 34). Но, как объяснялось ранее, в «Десяти шагах» обычно используются учебные задачи, основанные на реальных задачах, и такие обычные задачи приобретают форму плохо структурированных проблем.

Таблица 4.3 Краткое описание задачи, цели (целей), приемлемого решения и процесса решения проблемы для пяти реальных задач

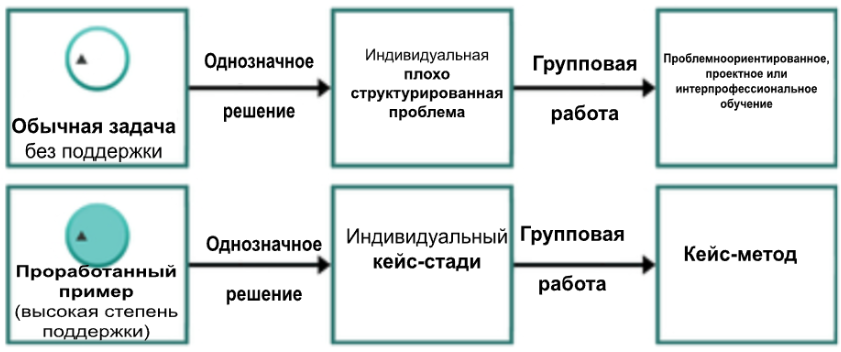
Рис. 4.6 Различные типы обычных задач и проработанных примеров

Обычная задача может быть выполнена отдельным учащимся или группой. Мы часто видим группу учащихся, выполняющих задачу — хотя это не обязательно должно быть строго необходимо — в проблемно-ориентированном обучении, где решение часто принимает форму объяснения конкретного явления (Loyens et al., 2011), в проектно-ориентированном обучении, где решение принимает форму совета или проектирования или производства продукта, который отвечает на исследовательский или практический вопрос (Blumenfeld et al., 1991), или в интерпрофессиональном обучении, где учащиеся из разных профессиональных областей выполняют профессиональную задачу в команде (Hammick et al., 2007). Эти типы группового обучения могут быть либо совместными (т. е. когда существует взаимозависимость задач, так что ни один человек в команде не может работать полностью независимо от других), либо кооперативными (т. е. когда у каждого члена команды есть определенная задача, которую нужно выполнить независимо от других членов команды; Kirschner et al., 2004).

На другом конце континуума проработанный пример обеспечивает наивысший уровень поддержки. Этот тип задачи сталкивает учащихся с заданным состоянием, целевым состоянием и полным решением, которое нужно изучить или оценить. Как и обычные задачи, проработанные примеры бывают разных форм, в зависимости от их структуры и/или неоднозначности и учащегося. Проработанные примеры, основанные на реальных задачах, часто принимают форму исследований случаев или случаев (см. нижнюю часть рисунка 4.6). Обычно это называется методом кейсов, когда группа учащихся — хотя это не обязательно должно быть строго необходимо — изучает кейсы (Barnes et al., 1994; для примера на основе 4C/ID см. Daniel et al., 2018). Хорошо продуманное исследование кейса представляет учащимся описания реальных или гипотетических проблемных ситуаций, существующих в реальном мире, и требует от них активного участия в данном решении; например, прося их критиковать данное решение или генерировать альтернативное решение (Ertmer & Russell, 1995).

Для примера видеопроизводства, представленного в главе 2, исследование случая может сталкивать учащихся с инструктажем клиента, а также информацией о доступности ресурсов и оборудования (т. е. «данное состояние»), желаемой целью для конечного видео с его продолжительностью и качеством производства (т. е. критерии для «целевого состояния»), отработанными примерами промежуточных решений (например, производственные планы, сценарии, раскадровки, кадры) и окончательным решением с завершенным и смонтированным видео (т. е. «решение»; см. верхнюю строку таб. 4.4). Чтобы вызвать интерес, может быть желательно использовать исследование случая, описывающее впечатляющую историю успеха или неудачи. Например, исследование случая может представлять собой рекламный ролик, который полностью провалился, потому что целевая аудитория неправильно его поняла. Хорошо продуманное исследование случая потребует от учащихся ответов на вопросы, которые вызывают глубокую обработку состояния проблемы и решения, и сравнения этого случая с другими случаями, чтобы вызвать обобщенные решения. Изучая (промежуточные) решения, учащиеся могут получить четкое представление об организации определенной области. В нашем примере они получают хорошее представление о структуре раскадровок и сюжетных линий.

В «Десяти шагах» выделяются еще несколько типов учебных задач, которые с точки зрения встроенной поддержки задач находятся между обычными задачами (плохо структурированными проблемами) и проработанными примерами (кейс-стади). Как показано в таблице 4.4 в колонках «Дано», «Цель» и «Решение», такие учебные задачи можно создавать путем манипулирования исходной информацией, целевым состоянием и решением.

Например, в обратном кейсе представлены и цель, и приемлемое решение (обозначенное знаком плюс), но учащиеся должны проследить цепочки последствий для различных ситуаций, то есть найти исходное состояние. В контексте поиска и устранения проблем Хафф (1993) описывает задачи, обратные задачам поиска и устранения проблем, — например, задачи, в которых учащимся сообщают, что определенный компонент работает некорректно или вышел из строя, и требуется найти исходное состояние — то есть состояние, которое позволит поставить данный диагноз. Как и кейс-стади, обратные кейсы концентрируют внимание учащихся на полезных решениях и требуют от них соотнести шаги решения с заданными ситуациями.

Задачи с неконкретной целью (также называемые задачами без цели; Ayres, 1993) стимулируют учащихся исследовать связи между решениями и целями, которых эти решения могут достичь. Обычно учащиеся получают задачи с конкретной целью, например, «Автомобиль массой 950 кг, разгоняясь по прямой из состояния покоя в течение 10 секунд, проезжает 100 метров. Какова конечная скорость автомобиля?» Эту задачу можно легко сделать неконкретной, заменив последнюю строку на «Вычислите значение как можно большего числа переменных, участвующих здесь». Здесь учащийся должен не только вычислить конечную скорость, но также ускорение и силу, оказываемую автомобилем при максимальном ускорении. А если слово «вычислить» заменить на «представить», учащийся также может включить графики и тому подобное. Задачи с неконкретной целью побуждают учащихся двигаться вперед от данностей и исследовать проблемное пространство, что может помочь им построить когнитивные схемы, в отличие от обычных задач с конкретной целью, которые заставляют учащихся работать в обратном направлении от цели. Работа в обратном направлении — это обременительный процесс для новичков, который может затруднить построение схемы (Sweller et al., 1998, 2019).

Таблица 4.4 Примеры различных типов учебных заданий для сложного навыка «создание видеоконтента» упорядочены от высокой поддержки задания (т. е. отработанный пример) до отсутствия поддержки задания (т. е. традиционная задача). Знак плюс (+) в столбцах «Дано», «Цель» и «Решение» означает, что этот аспект представлен обучающемуся; обозначение (например, предсказать) обозначает требуемое действие от обучающегося.

Задачи на завершение дают учащимся заданное состояние, критерии цели и частичное решение. Затем учащиеся должны завершить частичное решение, определяя недостающие шаги и добавляя их в решение. Особенно важно, что учащиеся при этом должны внимательно изучить предоставленное частичное решение — без этого они не смогут прийти к полному решению. Задачи на завершение особенно полезны в проблемных областях, ориентированных на проектирование, и первоначально были разработаны в области программной инженерии (Van Merriënboer, 1990; Van Merriënboer & de Croock, 1992), где учащиеся должны были вставлять недостающие командные строки в компьютерные программы. Решая хорошо продуманную задачу на завершение, учащиеся должны понять частичное решение и при этом выполнить нетривиальное завершение.

Как правило, все эти виды учебных задач направляют внимание учащихся на исходное состояние, приемлемые решения и полезные шаги решения. Это помогает учащимся мысленно абстрагировать информацию, связанную с правильными решениями, или использовать индуктивные процессы для построения когнитивных схем, которые позволяют находить обобщенные решения для конкретных типов задач. Исследования, посвященные учебным задачам с поддержкой или руководством, убедительно доказали, что такие задачи способствуют построению схем и переносу обучения на реальную жизнь у начинающих учеников (обзор см. в Van Merriënboer & Sweller, 2005, 2010). Оказывается, самостоятельное решение учащимися ряда задач не обязательно является лучшим способом обучения (Kirschner, Sweller, & Clark, 2006; Sweller, Kirschner, & Clark, 2007)! Гораздо полезнее, чем решение эквивалентных задач, для начинающих учеников может быть изучение хорошо проработанных примеров (кейс-стади). И лишь более опытные учащиеся, которые уже наработали большинство когнитивных схем, необходимых для разрешения проблем, должны решать обычные задачи.